Tutorial: Assessing coupling dynamics
In this tutorial we will characterize coupling dynamics between several scalar time-series using function transfer_entropy_pt.m, which is included in TIM Matlab interface. It is highly recommended that you go through the user documentation of TIM before trying to follow this tutorial.
Tutorial files
Here we provide the Matlab scripts that are used in this tutorial. We also include pre-computed results for each step of the tutorial (time-series generation, partial transfer entropy computation, final analysis figures).
Data generation
We consider the following non-linearly coupled Gaussian processes with a time-varying coupling factor:
''x^{(r)}[n] = 0.4x^{(r)}[n-1]+eta_x''
''y^{(r)}[n] = 0.5y^{(r)}[n-1]+kappa_{yx}[n]sin(x^{(r)}[n-tau_{yx}])+eta_y''
''z^{(r)}[n] = 0.5z^{(r)}[n-1]+kappa_{zy}[n]sin(y^{(r)}[n-tau_{zy}])+eta_z''
where the index ''r=1,...,50'' corresponds to the trial (or repetition) index and ''n=1,...,1500'' denotes time instants. The terms ''eta_x'', ''eta_y'' and ''eta_z'' are normally distributed noise processes, which are mutually independent across trials and time instants. The coupling delays are fixed to ''tau_{yx}=10'', ''tau_{zy}=15'' and the coupling strength is modulated using the following time-varying coupling factors:
''kappa_{yx}[n]={(sin(0.004pi n), for 250 <= n <=750),(0,otherwise):}''
''kappa_{zy}[n]={(cos(0.004pi n), for 750 <= n <=1250),(0,otherwise):}''
You could write yourself a Matlab script to generate these time-series. We have done this for you so you just need to type the following Matlab command:
>> data = gaussian_process;
where data is a cell array of dimensions 3 x 50. The rows of this cell array correspond to the x, y, and z time-series and the columns contain different random repetitions.
Measuring information transfer
Let us assume that we have measured ''x^{(r)}[n]'', ''y^{(r)}[n]'' and ''z^{(r)}[n]'' and that we want to infer the underlying connectivity pattern and the corresponding coupling dynamics. Before anything else, we have to reconstruct the state-space of these scalar time-series, which can be done using delay embedding:
>> Sx = delay_embed(data(1,:), dim, tau);
>> Sy = delay_embed(data(2,:), dim, tau);
>> Sz = delay_embed(data(3,:), dim, tau);
where dim and tau are the embedding dimension and the embedding delay, respectively. Choosing the right embedding parameters can be a tricky issue. The simplest way is to take tau = 1 and successively embed in higher dimensions until the results of the analysis are consistent. However, there are several more advanced techniques that you may want to try. For a comprehensive review on delay embedding and state-space reconstruction, we recommend you this book by Holger Kantz and Thomas Shreiber, two well-known experts in the field.
In our case, the default choice of tau = 1 and dim = 1 will produce satisfactory results, as we will see later. For convenience, we shall define here a lambda function (or function_handle using Matlab's terminology) as follows:
>> estimator = @(x, lag) transfer_entropy_pt(x(1,:), ...
x(2,:), x(3,:), x(4,:), 5, 0, lag, 0, 0, 20);
This lambda function bundles together the chosen information measure transfer_entropy_pt.m with its associated input parameters (timeWindowRadius = 5 samples, k = 20 nearest neighbors). Usually, time-varying estimates of information theoretic measures will have a large temporal variance. If you assume that the coupling dynamics are relatively slow, you can reduce the variance by simply smoothing the estimates e.g. with a moving average filter. In order to incorporate this post-processing step, we further define the following lambda function:
>> estimator_smooth = @(x, lag) filter(1/20*ones(1,20), 1, ...
estimator(x,lag), [], 2);
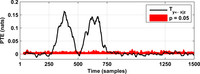
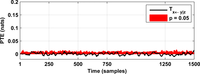
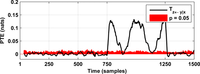
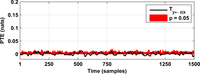
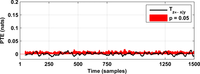
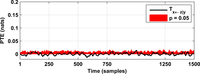
Now we are ready to measure information flow e.g. from system Sx towards system Sy using the partial transfer entropy (PTE):
>> W = delay_embed_future(Sy);
>> pte21 = estimator_smooth([Sy;Sx;Sz;W], 9);
where the first command builds the future of Sy. The delay of Sx should be such that the mutual information with W is maximized. By construction of our toy dataset, the lag that optimally aligns Sx and W is equal to ''tau_{yx}-1=9'' samples. If you do not know the optimum value a priori then you should compute the mutual information between Sx and W for multiple candidate lags using function mutual_information.m.
Significance threshold
Typically, a coupling analysis starts from the null hypothesis that the systems under study are uncoupled and the goal of the analysis is to prove otherwise. However estimators are not perfect and the number of data samples is finite, which explains why PTE estimates are almost never exactly zero. But then, how large should the PTE be to reject the null hypothesis? Determining this significance threshold analytically is difficult so we take instead a brute-force approach. We generate many surrogate datasets that resemble the dynamics of the original data but that, at the same time, are surely uncoupled. Say that you generate 20 such surrogates and that you compute the PTE for each of those surrogates. Let us then assume that the maximum (in absolute value) PTE estimate that you obtained was 0.15 nats. That is, if the true PTE is 0 nats you will get a PTE estimate above 0.15 nats in less than 5% of the occasions. Then, if you find from your original data a PTE estimate above 0.15 nats, you could say that the information flow is significant and has a p-value of 0.05, meaning that you have less than 5% chances of being wrong.
We can generate the uncoupled data surrogates by simply shuffling the data trials. Let us assume that we had only two repetitions of the time-series ''x^{(r)}[n]'', ''y^{(r)}[n]'' and ''z^{(r)}[n]'', i.e. let us assume that r = 2 in the equation describing the dynamics of our simulated dataset. Then, a disconnected surrogate of our time-series would be:
>> surrogate = {Sx{1,1} Sx{1,2};Sy{1,2} Sy{1,1};Sz{1,1} Sz{1,2}}
Since Sx{1,1} and Sy{1,2} correspond to different data trials, we know for sure that they are uncoupled. At the same time, the original data and the surrogate are very similar because different data trials have similar dynamics. All this process for determining the significance threshold can be easily done in TIM with the commands:
>> pte21_sig = permutation_test([Sy; Sx; Sz; W], [1 2 1 1], ...
@(x) estimator_smooth(x, 9), 0.05);
The last input parameter to function is the significance level or p-value. Note that the smaller the p-value, the more repetitions of the time-series are necessary for generating enough uncoupled surrogates. Following the example above, if you had only two trials, the minimum p-value that you could use would be p = 0.5. In a real study you should use p-values not greater than 0.05. The second input parameter of function permutation_test.m is a vector of indices that determines how to shuffle the data trials. Only system variables corresponding to different index values will be shuffled. That is, the value [1 2 1 1] in the code above means that the first and second variables (Sy and Sx) should be shuffled with respect to each other but Sy, Sz and W should all correspond to the same data trial. See the help of permutation_test.m and permute_pset.m for further explanations.
Results
After assessing all possible directions of information transfer, we have obtained the following figures:
These figures can be reproduced in MATLAB with the commands:
>> tutorial_gauss_data; % generate the time-series
>> tutorial_gauss_analysis; % estimate temporal PTE
>> tutorial_gauss_figures; % generate the figures
Credit
German Gomez-Herrero wrote this tutorial.
Kalle Rutanen helped with editing, proofreading, and testing the tutorial scripts.